什么是对数函数?
在数学中,对数函数是指以一定底数 b 为底数的指数函数,通常用“log”表示,如下所示:
logb x = y
在这个函数中,x是函数的输入(也就是函数的自变量),y是函数的输出(函数的因变量),b表示底数,表示对数运算的基准。
对数函数的定义范围
在定义对数函数的范围时,我们需要考虑到底数、自变量和函数值的限制因素。对数函数中,底数b必须大于0且不等于1(b>0, b≠1),自变量x必须大于0(x>0),而函数值y可以为所有实数(y∈R)。
换句话说,对于任何的b和x,对数函数都有定义,且函数值为实数集合中的一个数。
对数函数的定义域
接下来,我们来探究对数函数的定义域。
在对数函数中,自变量 x 必须大于 0,这是因为对数函数的定义是建立在指数函数的基础上的。指数函数中,底数不能为 0 或负数,否则指数函数就无法定义。
对数函数的本质是指数函数,将指数函数反过来,使底数变成原来的函数值,指数变成自变量。因此,对数函数的定义域实际上就是指数函数的值域。
例如,对于自然对数函数 y = ln x,指数函数 y = ex 的值域为 (0, +∞),因此定义域为 (0, +∞),即 x∈(0, +∞)。
同样地,以底数为 2 的对数函数 y = log2x 的定义域也为 (0, +∞),因为以 2 为底的指数函数 y = 2x 的值域也是 (0, +∞)。
对数函数的图像
了解对数函数的定义范围和定义域后,我们还可以通过绘制对数函数的图像来更深入地了解这个函数。
对于大多数的对数函数,随着自变量的增加,函数值会逐渐增加但增长速度逐渐减缓。这是因为随着 x 的增加,因变量 y 的增长速度会减缓。
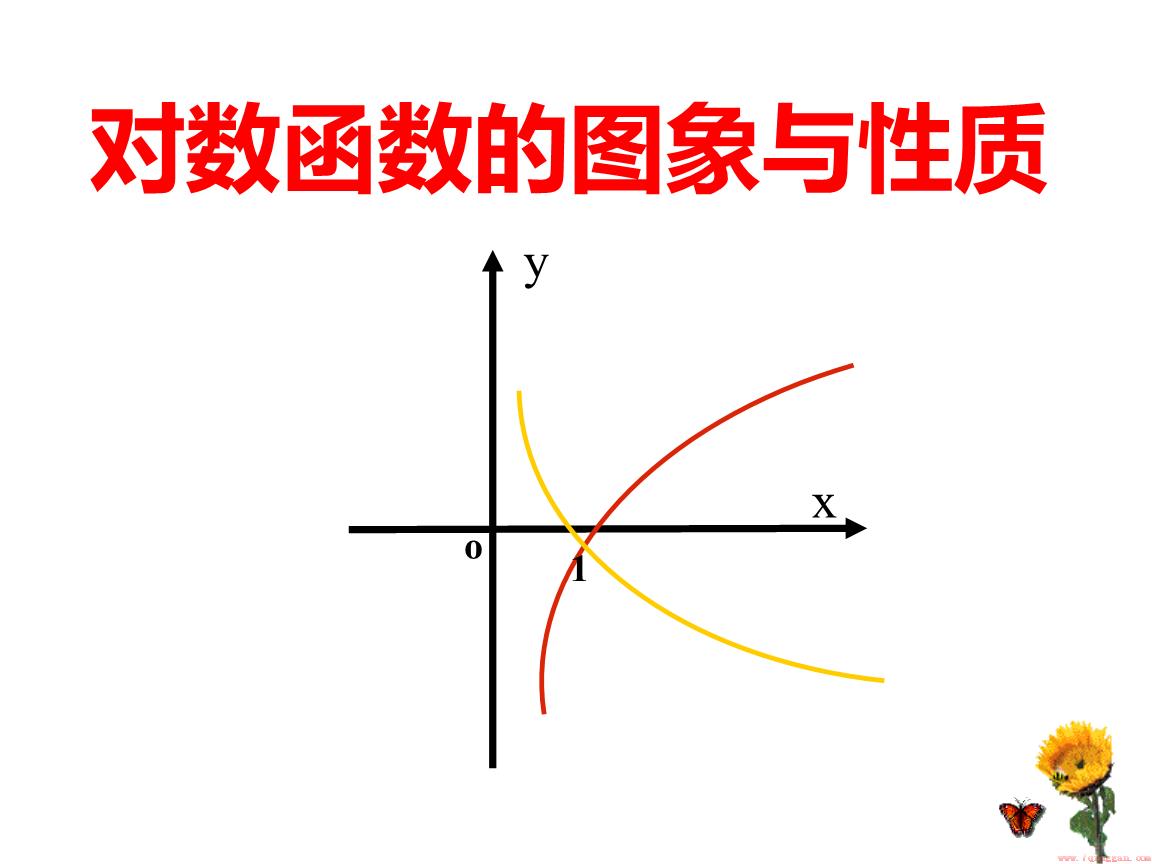
以底数为 2 的对数函数 y = log2x 为例,其图像如下所示:
如上图所示,对数函数的图像呈现出一个渐进线,这个线的斜率会趋近于 0。这就是对数函数随着自变量增加,增长速度逐渐减缓的原因。
总结
对数函数是以一定底数 b 为底数的指数函数,函数的定义范围主要是底数、自变量和函数值的限制因素,而函数的定义域则与指数函数的值域有关。了解对数函数的定义范围和定义域,可以更好地掌握该函数的数学特性,进而更好地应用到实际问题中。











评论列表