在数学中,子集是一个非常重要的概念。它描述了一个集合中的元素如何被另一个集合所包含。在这篇文章中,我们将详细讨论非空真子集和非空子集的概念,并通过实例进行解释。
首先,我们需要理解什么是子集。子集是原集合的一部分,也就是说,子集中的每一个元素都是原集合的元素。例如,如果我们有一个集合{1,2,3},那么它的所有子集包括{}、{1}、{2}、{3}和{1,2}等。
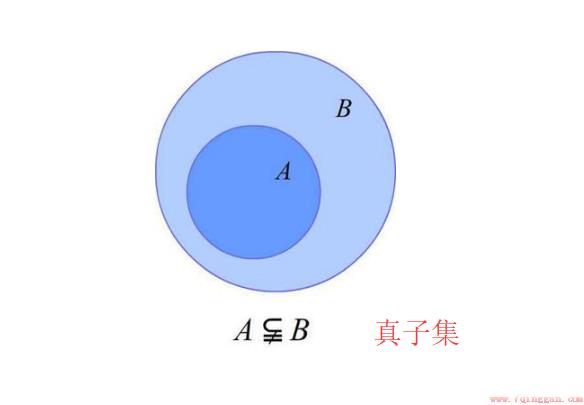
然而,子集的概念并不止于此。我们还可以进一步区分子集的类型。这就引出了我们今天的主题:非空真子集和非空子集。
非空真子集是指一个集合中的所有元素都不在另一个集合中出现。换句话说,如果A是非空真子集,那么A的所有元素都属于B,但A不等于B。
例如,假设我们有两个集合A={1,2}和B={1,2,3,4}。那么A就是B的一个非空真子集,因为A的所有元素都在B中,但A并不等于B。
非空子集则是指一个集合至少有一个元素。这与空集(没有任何元素的集合)形成对比。例如,如果我们有一个集合A={1,2,3},那么A就是一个非空子集,因为它至少有三个元素。
现在,让我们通过一些实例来更好地理解这两个概念。
假设我们有一个集合S={1,2,3,4,5}。
那么S的所有可能的非空子集包括{1}、{2}、{3}、{4}、{5}、{1,2}、{1,3}、{1,4}、{1,5}、{2,3}、{2,4}、{2,5}、{3,4}、{3,5}、{4,5}和{1,2,3}、{1,2,4}、{1,2,5}、{1,3,4}、{1,3,5}、{1,4,5}、{2,3,4}、{2,3,5}、{2,4,5}、{3,4,5}和{1,2,3,4}、{1,2,3,5}、{1,2,4,5}、{1,3,4,5}、{2,3,4,5}和{1,2,3,4,5}。
我们可以看到,这些非空子集中的每一个都至少有一个元素,而且没有一个元素出现在其他非空子集中。
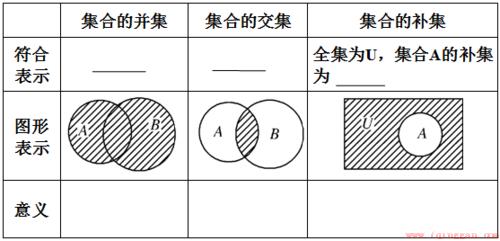
另一方面,S的所有可能的非空真子集包括{}(虽然这是一个空集,但它仍然是一个非空真子集,因为它没有出现在S中的元素)。
通过这些例子,我们可以看到非空真子集和非空子集的区别。非空真子集是指一个集合中的所有元素都不在另一个集合中出现,而非空子集则是指一个集合至少有一个元素。
这两种类型的子集在数学中都有广泛的应用,例如在组合学、概率论和统计学等领域。

评论列表